ตรรกศาสตร์

Posted by : Antioch วันอังคารที่ 15 กันยายน พ.ศ. 2558

Logical Agent

มีฐานความรู้ของตนซึ่งเป็นชุดของประโยคที่แสดงออกในความรู้ภาษาเป็นตัวแทน
ตัวแทนตรรกะสามารถเพิ่มประโยคใหม่เพื่อ KB รวมทั้งใช้ในการตอบคำถามสรุปมาจาก KB รับประกันได้ว่าจะถูกต้องหาก KB ที่ถูกต้อง
อนุมาน: อันเกิดประโยคใหม่จากที่มีอยู่

Ex: โจอี้เป็นสุนัข; สุนัขเป็นสัตว์; โจอี้จึงเป็นสัตว์

โจทย์

Propositions: assertions, statements

เป็นเรื่องที่สามารถเป็นจริงหรือเท็จ
ตัวอักษรเป็นทั้งสัญลักษณ์หรือสัญลักษณ์เชิงลบ

Ex: P, ~Q

Ex:“โจอี้เป็นสุนัข” P

“สุนัขเป็นสัตว์” Q

“ฉันมีสองแอปเปิ้ล” S

ตัวดำเนินการทางตรรกศาสตร์

~ not (negation, sometimes written ~) ปฎิเสธ

Λ and (conjunction)ตัวเชื่อม

V or (disjunction)

↔ if and only if ถ้าแล้ว

ลำดับความสำคัญ (สูงสุดไปต่ำสุด):~, Λ, V, , ↔

ถูกต้อง(Valid)

คำสั่งที่ถูกต้อง (หรือเราบอกว่าเป็นคำสั่งซ้ำซาก) ถ้าหากคำสั่งที่เป็นความจริง เพื่อทดแทนที่เป็นไปได้ของตัวแปรของพวกเขา
Ex: (พีวีพี ~) เป็นซ้ำซาก

p ~p p V ~p

T F T

F T T

Unsatisfiable

คำสั่งเป็น unsatisfiable (หรือเราบอกว่าคำสั่งที่เป็นความขัดแย้ง) ถ้าหากว่าคำสั่งที่เป็นเท็จเพื่อทดแทนที่เป็นไปได้ใด ๆตัวแปรของพวกเขา
Ex: (P Λ ~ P) เป็นความขัดแย้ง

p ~p p Λ ~p

T F F

F T F

Satisfiable(ความพอใจ)

คำสั่งคือ satisfiable (พอใจ)ถ้าหากว่า

คำสั่งที่เป็นจริงสำหรับอย่างน้อยหนึ่งที่เป็นไปได้

ทดแทนของตัวแปรของพวกเขา

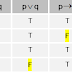
Ex: ทั้งสอง (pΛ q) (p V q) มีความพอใจ

p q p Λ q p V q

T T T T

T F F T

F T F T

F F F F

ประพจน์ตรรกะสมมูล (Logical equivalent)

De Morgan’s Laws (กฎของมอร์แกนเดอ)

~(p Λ q) ≡ ~p V ~q

~(p V q) ≡ ~p Λ ~q

Transformation(การเปลี่ยนแปลง)

p q ≡ ~p V q

Contrapositive

p q ≡ ~q ~p

Propositional Logic(ตรรกะของประพจน์)

“โจอี้เป็นสุนัข” P

“สุนัขเป็นสัตว์” Q

“โจอี้เป็นสัตว์” R

“โจอี้เป็นสุนัข; สุนัขเป็นสัตว์; โจอี้จึงเป็นสัตว์”

(P Λ Q) --> R

ดังนั้นวิธีการที่สามารถประโยคตรรกะเหล่านี้ช่วยให้เราแก้ปัญหา?

Entailment

Entailment: ประโยคจากเหตุผลดังต่อไปนี้อื่น

KB ╞ α

ฐานความรู้ของ KB ที่มีรายละเอียดαประโยคถ้าหากαเป็นความจริงในโลกทั้งหมดที่ KB ที่เป็นความจริง

Ex: x + y = 4 entails y + x = 4

Proof by contradiction(การพิสูจน์โดยข้อขัดแย้ง)

α ╞ β iff (α Λ ~β) is unsatisfiable

นั่นคือสมมติว่าเรารู้ว่าαเราสามารถพิสูจน์βโดยแสดงให้เห็นว่า (αΛ ~ β) ไม่สามารถเป็นจริง

ในคำอื่น ๆ ที่เราพิสูจน์ได้ว่าเป็นความจริงβโดยแสดงให้เห็นว่าถ้าβเป็นเท็จก็จะขัดแย้งกับα

Example 1

Given

(P Λ ~R) “พีทอยู่ที่นี่ "และ" รอนไม่ได้อยู่ที่นี่” (1)

(~Q R) “หากควีนไม่อยู่ที่นี่แล้วรอนอยู่ที่นี่” (2)

ต้องการที่จะพิสูจน์

Q “ควีนอยู่ที่นี่” (3)

หลักฐานจากความขัดแย้ง จำเป็นที่จะต้องแสดงให้เห็นว่าทุกการรวมกันของค่าความจริง P, Q, R, ไม่มีใครทำให้ประโยคต่อไปนี้เป็นความจริง

(1) Λ (2) Λ ~(3)

(P Λ ~R) Λ (~Q R) Λ ~Q

? เราได้แสดงให้เห็นว่า

(1) Λ (2) Λ ~ (3)
ไม่สามารถที่จะเป็นจริง และเรากำลังได้รับว่าทั้งสอง (1) และ(2) เป็นจริง
ดังนั้น ~ (3) ต้องเป็นเท็จซึ่ง ทำให้ (3) ความจริงที่เราอยากจะพิสูจน์

Example 2

Given

Q R (1)

~(R P) Q (2)

P V R (3)

ต้องการที่จะพิสูจน์

P V Q (4)

หลักฐานจากความขัดแย้ง จำเป็นที่จะต้องแสดงให้เห็นว่าประโยคต่อไปนี้ไม่สามารถเป็นจริง

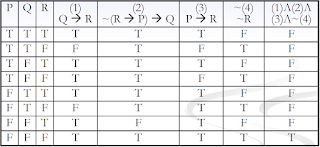
(1) Λ (2) Λ (3) Λ ~(4)

(1) Λ (2) Λ (3) Λ ~(4)มักจะเป็นเท็จและ(1), (2), (3)เป็นจริง ดังนั้น(4)ต้องเป็นจริงตามที่ต้องการ

Example 3

Given

Q R (1)

~(R P) Q (2)

P R (3)

ต้องการที่จะพิสูจน์

R (4)

(1) Λ (2) Λ (3) Λ ~(4)

สามารถเป็นจริงหรือเท็จ เราไม่สามารถพิสูจน์ได้ว่าเป็นความจริง R

Conjunctive Normal Form

ประโยคที่อยู่ในรูปแบบปกติที่เชื่อมต่อกัน (CNF) ถ้ามันจะแสดงเป็นร่วมของ disjunctions ของตัวอักษร

(literal1 V ... V literali) Λ ... Λ (literalj V ... V literalk)

ประโยคของประพจน์ลอจิกทุกคนสามารถเป็นกลายเป็น CNF
วิธีการเปลี่ยนประโยคเป็น CNF
R ↔ (P V Q)

1. แทนที่ (α ↔ β) กับ (α β) Λ (β α)

(R (P V Q)) Λ ((P V Q) R)

2. แทนที่ (α β) กับ(~α V β)

(~R V (P V Q)) Λ (~(P V Q) V R)

Resolution(ความละเอียด)

มติที่จะใช้เวลาสองข้อ CNFและสร้างประโยคใหม่ที่มีตัวอักษรทั้งหมดของทั้งสองคำสั่งเดิมยกเว้นสองตัวอักษรเสริม

Ex: Given: (A V B) Λ (~B V C)

ผลลัพธ์: A V C

(A V B) Λ (~B V C)หมายถึงA V C (แต่ไม่ได้อยู่ในทางกลับกัน)

1 แปลง ~ αและคำสั่งจาก KB ที่จะ CNF

2. แต่ละคู่ที่มีตัวอักษรที่สมบูรณ์คือ มีมติในการผลิตคำสั่งใหม่ซึ่งเป็นเพิ่มไปยังชุดถ้ามันไม่ได้อยู่แล้วต่อไปจนกว่าหนึ่งในสองสิ่งที่เกิดขึ้น:

? ไม่มีคำสั่งใหม่ที่สามารถเพิ่มที่ กรณี KB ไม่ตกทอดαหรือ
? การประยุกต์ใช้กฎความละเอียดที่มา ข้อที่ว่างเปล่าในกรณีที่ส่งผล KB α

ไม่มีคำสั่งที่ต้องทำ ความละเอียด--> ไม่สามารถที่จะ พิสูจน์ให้เห็นว่า R เป็นความจริง

First-Order Logic

ปัญหาเกี่ยวกับลอจิกประพจน์: ไม่ที่แสดงออกพอ
ในโลกที่ลอจิกประพจน์มีข้อเท็จจริงอยู่
ในโลกครั้งแรกที่สั่งซื้อลอจิกมีข้อเท็จจริงอยู่วัตถุและความสัมพันธ์
FOL เป็นที่แสดงออกมากขึ้น เราสามารถมีประโยคกับตัวแปรและฟังก์ชั่น

Universal Quantifier

"สำหรับทุกอย่าง ... "

Ex:

สำหรับ x ทุกคนถ้า x เป็นเด็ก x ชอบไอศครีม

เด็กขวาน (x)? ชอบ (x, ไอศครีม)

สำหรับ x ทุก x เป็นทั้งสีเหลืองหรือสีเขียว (หรือทั้งสอง)

Ax เหลือง (x) กรีน V (x)

Existential Quantifier(E)

อัตถิภาวปริมาณ

"สำหรับบางคน ... " หรือ "มีอยู่ ... "
Ex: มีเด็กบางคนที่ไม่ชอบผัก (E)

อดีตเด็ก (x) Λ ~ ชอบ (x, ผัก)(E)
มี x บางอย่างเช่นว่าถ้ากินผักขม x คือ x
จะกลายเป็นที่แข็งแกร่ง
อดีตกิน (x, ผักโขม)? ที่แข็งแกร่ง (x)

Nested Quantifier

ปริมาณที่ซ้อนกัน
ทุกคนมีคนที่เขา / เธอชอบ

Ax Ey มนุษย์ (x) Λมนุษย์ (y) Λชอบ (x, y) ขวาน

มีคนที่ทุกคนชอบคือ

Ax มนุษย์ (x) Λมนุษย์ (y) Λชอบ (x, y)

Negation

และการปฏิเสธ

การเชื่อมต่อระหว่าง

ชอบขวาน (x, IceCream)

ขวาน ~ ~ ชอบ (x, IceCream)

อดีต ~ ชอบ (x, IceCream) ~

ทุกคนชอบไอศครีม

ไม่มีใครที่ไม่เป็น

บางกฎ

ไม่ชอบไอศครีม

Ax ≡≡ E ~ ~ Ex x ขวาน

CNF in FOL

วิธีการเปลี่ยนประโยคเป็น CNF

Resolution in FOL

ในขณะที่ลอจิกประพจน์เพื่อที่จะใช้ความละเอียด FOL ต้องใช้ประโยคที่จะอยู่ใน CNF
ความละเอียด: คล้ายกับผู้ที่อยู่ในลอจิกประพจน์ แต่มีตัวแปร / ทดแทนอย่างต่อเนื่อง
ได้รับ Au, v, x, y
กิน (x, y)? ล่า (x, y)
ล่า (ยูวี) ~ ล่า (V, มึง)
? ต้องการที่จะพิสูจน์
(1) ถ้าฉันกินคุณฉันล่าคุณ
(2) ถ้าฉันล่าคุณคุณไม่ล่าฉัน
น้ำหนัก ~ กิน (สิงโตน้ำหนัก)
? นั่นคือพิสูจน์ว่า (1) Λ (2) Λ ~ (3) เป็น unsatisfiable
(3) มีสิงโตบางสิ่งบางอย่างที่ไม่ได้กิน
ตัวอย่างเครดิต: สเวนนิก

Subscribe to Posts | Subscribe to Comments

AI

Please Wait . . .