AI

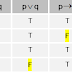
เป็นเกมส์ผลรวมเป็นศูนย์ เนื่องจากผลรวมนี้คือการรวมความสำเร็จ ชนะพร้อมกันไม่ได้
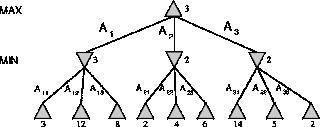
1. ขั้นตอนวิธีแบบค่าน้อยสุด-มากสุด minimax algorithm จุด root node แทนผู้เล่นแรกๆ และจุดโหนดลูกแทนผู้เล่นฝ่ายตรงข้าม จุดปลายสุดจะระบุคะแนน เราต้องหาการเล่นวิธีที่ดีดีที่สุดของผู้เล่นคนแรกดังนั้น จึงเลือกคะแนนสูงสุดต่อจุดของจุดต่อลูกๆๆของมัน ส่วนที่จุดต่อของผู้เล่นฝั่งตรงข้ามจะเลือกคะแนนสูงสุดของจุดต่อลูกๆมัน ส่วนจุดต่อฝั่งตรงข้ามจะเลือกคะแนนต่ำสุดของจุดลูกๆของมัน สำหรับจุดต่อที่น้อยที่สุดMIN คะแนนเริ่มแรกก่อนการเปรียบเทียบ จะเท่ากับ +infinityและลดลงเรื่อยๆเมื่อโปรแกรมทำงานต่อไป ส่วนจุดต่อมากที่สุด(MAX)คะแนนจะเริ่มที่-infinityและเพิ่มขึ้นเรื่อยๆ แผนถูมิต้นไม้ขนาดใหญ่จนต้องกำหนดขอบเขตล่วงหน้า

-สถานะ,เป้าหมาย,การกระทำ,ฟังก์ชั่นการแก้ปัญหาที่มีโดเมนที่เฉพาะเจาะจง

• Binary CSP: แต่ละข้อจำกัดที่เกี่ยวข้องกับสองตัวแปร
• Constraint graph: โหนดเป็นตัวแปรโค้งที่มีข้อจำกัด

e.g., SA ≠ WA

Higher-order: ข้อจำกัดที่เกี่ยวข้องกับมากกว่า3ตัวแปรขึ้นไป

Real-world CSPs

ปัญหาที่ได้รับมอบหมาย
=เช่นสิ่งที่สอนในชั้นเรียน
ปัญหา timetabling
=เช่น ระดับที่จะถูกนำเสนอเมื่อใดและที่ไหน

• การจัดตารางเวลาการขนส่ง
• การตั้งเวลาโรงงาน
• ขอให้สังเกตว่าปัญหาที่แท้จริงของโลกจำนวนมากที่เกี่ยวข้องกับมูลค่าที่แท้จริงตัวแปร

ค้นหาสูตรมาตรฐาน (เพิ่มขึ้น)Standard search formulation (incremental)

วิธีธรรมดาในการค้นหา
สถานะจะถูกกำหนดโดยค่าที่ได้รับมอบหมายเพื่อให้ห่างไกล

• สถานะเริ่มต้น: การกำหนดที่ว่างเปล่า {}
• ฟังก์ชั่นตัวตายตัวแทน (การกระทำ): กำหนดค่าให้ตัวแปรที่ไม่ได้กำหนดว่าไม่ขัดแย้งกับที่ได้รับมอบหมายในปัจจุบัน

• วิธีการใช้งานทั่วไปมีความเร็วมากในการรับ:
• ซึ่งตัวแปรควรจะกำหนดต่อไปหรือไม่
• ในสิ่งที่เรียงลำดับตามค่าที่พยายาม?
• เราสามารถตรวจสอบความล้มเหลวที่หลีกเลี่ยงไม่ได้ในช่วงต้น?

ตัวแปรที่จำกัดมากที่สุด

• การตรวจสอบการส่งต่อแพร่กระจายข้อมูลจากได้รับมอบหมายให้ตัวแปรที่ไม่ได้กำหนด แต่ไม่ได้ให้ตรวจสอบเริ่มต้นสำหรับความล้มเหลวทั้งหมด:
• NT และ SA ไม่สามารถทั้งเป็นสีฟ้า!
• การขยายพันธุ์อย่างจำกัด(Constraint propagation) ซ้ำบังคับใช้ข้อจำกัดในประเทศ มันแพร่กระจายผลกระทบของข้อจำกัด ในตัวแปรหนึ่งบนตัวแปรอื่น ๆ

Arc consistency(สอดคล้อง)

• รูปแบบที่ง่ายของการขยายพันธุ์ที่ทำให้โค้งแต่ละที่สอดคล้อง (consistent)กัน
• X--> Y ถ้ามีความสอดคล้อง
• สำหรับทุกค่า x ของ X มีบาง y ที่ได้รับอนุญาต
• การตรวจสอบความArc consistency ต้องใช้ซ้ำ ๆ จนกระทั่งไม่มีความไม่สอดคล้องกันมากขึ้นยังคงอยู่
• ถ้า x สูญเสียค่าใกล้เคียงของ X จะต้องมีการเดินทาง
• เช่นเมื่อ V สูญเสียค่าจะต้องตรวจสอบค่าของNSW และ SA’s จากนั้นจะต้องตรวจสอบค่าของNSW’s and SA’s และอื่น ๆ

Class	Name	Operation
ไม่รู้เส้นทางใด	Depth-First Breadth-First	ระบบการตรวจสอบข้อเท็จจริงของต้นไม้ ทั้งค้นหาจนกว่าจะพบเป้าหมาย
รู้เส้นทางเส้นทาง	Greedy Best- First	ใช้มาตรการแก้ปัญหาของความดีของสถานะ เช่น ระยะทางประมาณเป้าหมาย
ไม่รู้ความเหมาะสม	UniformCost	ใช้เส้นทาง "ความยาว" วัดพบ "สั้น" เส้นทาง
รู้ความเหมาะสม	A*	ใช้เส้นทาง"ความยาว" มาตรการและ การแก้ปัญหาพบเส้นทาง"สั้น"

• Uninformed search  :(หรือการค้นหาแบบตาบอด): ไม่มีเพิ่มเติมข้อมูลเกี่ยวกับสถานะเกินกว่าที่ระบุไว้ในคำนิยามปัญหา
•  Informed search :(หรือการค้นหาที่ Heuristicการค้นหาที่เลือกคำตอบที่เหมาะสมกับการค้นหาเท่านั้นแต่อาจจะไม่ใช่คำตอบที่ดีที่สุด): ใช้ problem- 7? ค้นหาแจ้ง (เทียบกับการแก้ปัญหาการค้นหา): ใช้ความรู้เฉพาะปัญหาที่นอกเหนือจากความหมายของปัญหาของตัวเอง
  

Informed (Heuristic) Search

• บางขั้นตอนวิธีการค้นหาที่ใช้heuristic functions.
• heuristic functionsอาจจะช่วยเป็นแนวทางในการค้นหาและเพิ่มความเร็วอย่างน้อยโดยเฉลี่ยกระบวนการในการหาที่เป้าหมาย
• การประเมินผลการใช้ฟังก์ชัน f (s) ซึ่งประมาณการระยะทางไปยังเป้าหมาย
• ขยายโหนดที่มีลักษณะที่ดีที่สุด (มีแนวโน้มมากที่สุด)ในขณะที่คนที่มีต่ำสุด f (s)
• เราจะหารือสองวิธี:

1. Greedy best-first search
2. A* search

Greedy Best-First Search

• ขยายโหนดที่ปรากฏขึ้นใกล้เคียงกับเป้าหมาย
• เลือกเส้นทางที่ดีที่สุดที่ดูจากโหนดปัจจุบัน S เพื่อเป้าหมาย
• f (s) = h (s)  h (s): ประเมินค่าใช้จ่ายของเส้นทางถูกที่สุดจากโหนดเพื่อเป้าหมาย
• h (เป้าหมาย) = 0

Greedy Best-First Search

• A* = สมบูรณ์ที่สุด,ดีที่สุด
• A * จะเสร็จสมบูรณ์และที่ดีที่สุดที่ได้รับ h (s) ตอบสนองเงื่อนไขบางประการ
• เงื่อนไขอะไร?--> h (s) เป็นที่ยอมรับ
• ดังนั้น เป็นปัญหาหรือไม่? -->หน่วยความจำ

ซ้ำที่ดีที่สุดครั้งแรกที่การค้นหา (RBFS)

เป็นการค้นหาแบบที่เริ่มต้นการสำวจจากโหนดหนึ่งไปยังอีกโหนดหนึ่งอาศัยทิศทางเป็นตัวกำหนดการค้นหา  ไม่มีข้อมูลอะไรมาเสริมการตัดสินใจ คือการหยิบข้อมูลมาตรวจสอบในขั้นต่อไป ไม่ต้องอาศัยข้อมูลใดๆทั้งสิ้น ตัวอย่าง Depth First Search ,Breadth First Search

เป้นการค้นหาแบบลึกก่อน กำหนดทิศทางจากรูปโครงสร้างต้นไม้ เริ่มจากRoot เดินลงมาที่ลึกสุดTerminal Node ให้ย้อนขึ้นไปที่กิ่ง แยกต่ำสุดของกิ่งเดียวกัน และยังไม่ทำการสำรวจแล้วทำการสำรวจโหนดในกิ่งนั้น ถ้าพบโหนดที่ต้องการการค้นหาก็สิ้นสุด ถ้าไม่พบก็สำรวจจนถึงปลายทาง  ถ้าไม่พบให้ย้อนขึ้นมายังกิ่งแยกต่ำสุดที่ยังไม่สำรวจถัดไปแล้วทำการสำรวจโหนดบนกิ่งแยกนั้น ทำสลับกับไปเรื่อยๆจนพบโหนดที่ต้องการหาหรือสำรวจให้ครบทุกโหนด

เป็นการกำหนดทิศทางการค้นหาที่ทำการสำรวจที่ละระดับของโครงสร้างต้นไม้ ดดยเริ่มจากโหนดรากแล้วลงมาที่ระดับ1จากซ้ายไปขวา จนกว่าจะพบโหนดที่ต้องการ หรือจนครบทุกโหนด เป้นหมายเลขที่กำกับบนโหนด 

จะอาศัยการจัดการโครงสร้างข้อมูลแบบคิวมาช่วย เช่นกัน ด้วยวิธีการเช่นเดียวกับการค้นหาแบบลึกก่อน คือให้เริ่มต้นสำรวจที่โหนดเริ่มต้น แล้วนำโหนดที่ข้างเคียงเก็บไว้ในคิว เมื่อสำรวจโหนดเริ่มต้นจนเสร็จ ให้นำข้อมูลในคิวออกมาสำรวจ นำโหนดข้างเคียงที่ไม่ได้สำรวจและไม่ได้อยู่ในคิวใส่ในคิว ทำจนพบโหนดที่ต้องการหรือเมื่อสำรวจครบทุกโหนด สำหรับโหนดข้างเคียงในที่นี้หมายถึงโหนดที่มีเส้นเชื่อม เชื่อมกับโหนดที่กำลังสำรวจหรือกล่าวอีกนัยหนึ่ง คือ โหนดที่อยู่ติดกันและมีทางเดินเชื่อมหากัน

การค้นหาแบบฮิวริสติก

        ความแตกต่างระหว่างการค้นหาข้อมูลธรรมดา และ การค้นหาข้อมูลแบบฮิวริสติก(Heuristic Search) การค้นหาแบธรรมดาจะเป็นการตรวจสอบข้อมูลจนครบ ถ้าข้อมูลไม่ใหญ่มาก การค้นหาแบบนี้จะให้คำตอบที่ถูกต้องเสมอ แต่ในบางครั้งข้อมูลมีขนาดใหญ่มาก การตรวจสอบต้องทำหลายล้านครั้ง ซึ่งทำให้การเปรียบเทียบข้อมูลทุกตัวเพื่อหาคำตอบที่เป็นไปไม่ได้  ลักษณะของปัยหาแบบนี้ เช่น การหาทางที่สั้นที่สุดเราจะต้องเปรียบเทียบเส้นทาง 99! ครั้ง หรือ (n-1)! เมื่อ n คือจำนวนเมืองซึ่งต้องการเปรียบเทียบจำนวนที่ไม่อาจเปรียบเทียบให้เสร็จได้ ดังนั้นจะตอบคำถามว่าเส้นที่สั้นที่สุดคือเส้นทางใด จะยากมากและอาจหาไม่ได้เลยก็ได้  ดังนั้นการแก้ปัญหาต้องอาศัยวิธีการฮิวริสติก วิธีการนี้เลือกคำตอบที่เหมาะสมให้กับการค้นหาเท่านั้น แต่ไม่ได้คำตอบที่ดีที่สุด
           เครื่องมือช่วยค้นหาฮิวริสติก คือ ฮิวริสติกฟังชัน
Heuristic Functionทำหน้าที่วัดขนาดความเป็นไปได้ในการแก้ปัญหา เพื่อกำหนดทิศทางของการค้นหาคำตอบ หรือกล่าวอีกนัยหนึ่งคือ ฮิวริสติกฟังชันจะเป็นการบอกว่าสำรวจครั้งต่อไปจะเลือกสำรวจโหนดที่กิ่งใด โดยบอกขนาดของความเป็นไปได้ และขนาดความเป็นไปได้แสดงเป้นตัวเลข
          การวัดความเป็นไปได้ในการแก้ปัญหา จะกระทำได้โดยพิจารณษถึงวิธีการ(Aspects)ต่างๆ  ที่ใช้ในการแก้ปัญหา ณ สถานะหนึ่งว่า จะสามารถแก้ปัญหาได้ตามที่ต้องการหรือไม่ โดยกำหนดน้ำหนักที่ให้กับการแก้ปัญหาของแต่ละวิธี น้ำหนักเหล่านี้จะถูกแสดงด้วยตัวเลขที่กำกับไว้โหนดต่างๆ ในกระบวนการค้นหา และค่าเหล่านี้จะเป็นตัวที่ใช้ในการประมาณความเป็นไปได้ว่าเส้นทางผ่านโหนดนั้น มีความเป็นไปได้นำสู่หนทางการแก้ปัญหาได้มากน้อยแค่ไหน

การค้นหาBest-first search

การค้นหาแบบเลือกโหนดที่ดีที่สุด (most promising) การทราบว่าโหนดใดดีที่สุดนี้สามารถทำได้โดยอาศัยฮิวริสติกฟังชั่น ฮิวริสติก ฟังชันนี้ทำหน้าที่เหมือนตัววัดผล

กรีดีอัลกอริทึมGreedy Algorithm

เลือกโหนดที่ดีที่สุดก่อน อาศัยการวัดสถานะไปยังเป้าหมาย ดังนั้นการเลือกโหนดต้องเลือกโหนดที่มีค่าh ดีที่สุด

เลือกโหนดที่ใช้ดำเนินการต่อที่ดีที่สุด  วิธีการเลือกโหนดที่ใช้ในการดำเนินการต่อ พิจารณาจากโหนดที่ดีที่สุด ความแตกต่างระหว่างA* กับฮิวริกฟังชั่น  ฮิวริกฟังชั่น จะวัดจากโหนดราก(เริ่ม) โหนดปัจจุบัน(สถานะปัจจุบัน) แต่ค่าฮิวริสติก ฟังก์ชั่นA*จะเกิดการรวมค่า2ค่า คือ ค่าวัดจากสถานะปัจจุบันไปยังสถานะเริ่มต้น รวมค่าที่วัดจากสถานะปัจจุบัยนไปยังสถานะเป้าหมายถ้ากำหนดให้ตัวแปร fแทนค่าของฮิวริสติก ฟังชันของA* และg เป็นฟังชันที่ใช้วัดค่า(cost)จากสถานะเริ่มต้นจนถึงสถานะปัจจุบัน h' เป็นฟังชั่นที่ใช้วัดค่าจากสถานะปัจจุบันถึงสถานะเป้าหมาย

การค้นหาข้อมูลแบบ A*ของปัญหา 8-Puzzle ในการคำนวณค่าของ g คือการเปรียบเทียบสถานะปัจจุบัน กับสถานะเริ่มต้น และค่า h' คือการเปรียบเทียบสถานะปัจจุบันกับสถานะเป้าหมาย ซึ่งในการคำนวณค่าgและh'

สถานะเริ่มต้น

สถานะเป้าหมาย

การหาค่าของ g ทำได้โดยเปรียบเทียบสถานะปัจจุบันกับสถานะเริ่มต้น คือการนับว่าแต่ละช่องของตารางปัจจุบันห่างจากจุดเริ่มต้นไปกี่ช่อง เช่นที่ช่อง1ตารางทั้งสองไม่ห่างกัน ดังนั้นได้ค่า0 ที่ช่อง1ที่ช่อง2 สถานะปัจจุบันไม่มีค่าไม่คิด และเช่นกันที่ช่องที่3และ4ก็มีค่าเป็น0 เพราะทั้งสองตารางไม่ต่างกัน สำหรับตารางที่5 จะมีค่าเป็น1เพราะ8ห่างจากที่เคยอยู่ 1 ช่อง ทำเช่นนี้เรื่อยๆเราจะได้คำตอบช่องตารางต่างๆ ดังนี้
1=0,2=0,3=0,4=0,5=1,6=0,7=0,8=1,9=0รวม g=2

สำหรับค่าของ h'จะได้
1=1,2=0,3=0,4=1,5=1,6=0,7=0,8=1,9=0รวมh'=3 f=2+3=5

ข้อสังเกต

Depth-First Search ตามแนวลึก

-เป็นวิธีที่ไม่ดี

-ไม่รับประกันว่าจะหยุด ถ้าต้นไม้มากมายก็ต้องค้นจากที่ลึกก่อน เพื่อแก้ไขปัญหานี้:Depth-Limited Search

Depth-Limited Search

• DFS ที่มีความลึกคงที่  โหนดที่ระดับความลึกไม่มีการสืบทอด
• อะไรคือสิ่งที่เหมาะสมcut-off depth d?
• ถ้า d มีขนาดเล็กเกินไปไม่อาจหาเป้าหมายได้
• ถ้า d มีขนาดใหญ่เกินไป: การทำงานพิเศษ
• สิ่งที่เกี่ยวกับการเริ่มต้นที่มีขนาดเล็กและให้ d เพิ่มขึ้น? 
• ซ้ำลึกการค้นหา

• ค้นหาลึกมากขึ้น
• DFS มีความลึกคงค่อยๆที่เพิ่มขึ้น
• มันไม่ซ้ำมากเกินไปในการทำงานหรือไม่
• ในต้นไม้เวลาถูกครอบงำโดยการค้นหาแนวลึกที่สุด(deepest search)

BFS Revisited

• การขยายตัว Node: A, B, C, E (เป้าหมาย)
• โซลูชั่นที่พบ: A-B-E  (ค่าใช้จ่าย 100) - ไม่ดีที่สุด
• การแก้ไขปัญหานี้: การค้นหาเครื่องแบบค่าใช้จ่าย

Uniform-Cost Search การค้นหาแบบประหยัดต้นทุน

• ขยายโหนดที่มีค่าใช้จ่ายในเส้นทางที่ต่ำที่สุด (ใกล้เคียงกับเป้าหมาย)
• เหมือนกับ BFS หากค่าใช้จ่ายขั้นตอนทั้งหมดเท่ากัน

• การขยายตัว Node: A, C, D, E (เป้าหมาย)
• โซลูชั่นที่พบ: A-C-D-E (ต้นทุน 3) - ที่ดีที่สุด
• ที่ดีสำหรับค่าใช้จ่ายที่ไม่สม่ำเสมอ

Bidirectional Searchการค้นหาสองทิศทาง

• การค้นหาพร้อมกันสองคนคนหนึ่งไปข้างหน้าจากสถานะเริ่มต้นย้อนหลังจากเป้าหมายอื่น ๆ
• ประหยัดพื้นที่

      การสร้างรูปแบบเครื่อข่ายข้อมูลกราฟ ดีกว่าต้นไม้ เพราะจะประหยัดพื้นที่หน่วยความจภำ การค้นหาข้อมูลทำได้เร็วกว่า ข้อเสีย ทำให้เชื่อมต่อของข้อมูลทำได้ยาก ใช้เวลาในการเชื่อมต่อข้อมูลนานกว่า ดังนั้นการออกแบบโครงสร้างบางครั้งจึงนิยมสร้างเป้นต้นไม้ก่อนแล้วค่อยเปลี่ยนเป็นกราฟ

การแสดงความรู้

Knowledge Representation เป้นวิธ๊การแสดงความรู้ในการแก้ปัญหาให้อยู่ในรูปแบบที่คอมพิวเตอร์ประมวลผลได้ การแสดงคสามรู้นี้จุะอยู่ในรูปประโยค และจะต้องสอดคล้องกันทั้งในแง่ของไวยากรณ์ ท Syntax และความหมาย Semantic
เงื่อนไข-->ข้อสรุป

ในกรณ๊ที่ความรู้ไม่ใช่ตัวเลข เป็นobjectและfact ที่มีความสัมพันธ์กัน เช่น ความรู้ "Plant is on the table พืชอยู่บนโต็ะ"
จะมีobject 2 ตัว  พืชและโต๊ะ มีonแสดงถึงความสัมพันธ์การแสะดงความรู้แบบนี้จะมีการกล่าวถึงต่อไปอย่างละเอียด

ON(plant,table):plant is on  the table
IN(table,room):table is in the room
UNDER (table,window)table is under the window

อย่างไรการแสดงความรู้มีสิ่งที่ควรคำนึงถึง
1.รวมความรู้เป็นหนึ่งเดียวกันได้อย่างไร เช่น ถ้าอธิบายลักษณะห้องห้องหนึ่ง ห้องนี้มีโต๊ะตั้งไว้ใต้หน้าต่าง table is under the window  แล้ววันหนึ่งมีการเปลี่ยนฐานความรู้ว่า CENTER (table,room)ในระบบแสดงความรู้มีวิธีการอย่างไรที่จะแจ้งให้ทราบว่าUNDER (table,window) ไม่ได้เพราะในเมื่อโต๊ะมาอยู่กลางห้องก็เป็นไปไม่ได้ทีโต๊ะจะอยู่ใต้หน้าต่างด้วย
2.จัดลำดับให้ค้นหาง่าย เช่น ถ้าเติมABOVE(ceiling,floor)เข้าไปในฐานความรู้ ใส่ตรงไหนที่จะไม่ต้องบอกทุกครั้งเมื่อมีการอ้างถึงว่า เพดานอยู่เหนือพื้น

ทั้งหมดที่กล่าวมานี้เป็นการแสดงความรู้ด้วยเฟรม(frame)